這個模型大概已經被人講過很多次，講到都快要爛掉了XD

其實我自己在兩年前的鐵人賽中也有講過同一個模型，所以我就不用講太多基礎的部份：

總的來說，線性模型就是依賴著 $y = w_0 + w_1x_1 + w_2x_2 + \dots + w_nx_n$ 這樣的一條數學式子。

為了方便起見我們將他化成向量的形式：$$y = \mathbf{w}^T\mathbf{x} + b$$

你會發現線性迴歸會是一個向量的內積的運算再加上一個常數，這個常數被很多人討論很久，很多人可能不是那麼了解他的意義。這個常數代表的就是在空間上的一個位移，在內積的 $\mathbf{w}$ 這個係數向量上，他們決定了在空間中整個線或是平面的傾斜程度，而常數則是在空間上的位移，也就是要將這個線或是平面擺在哪一個地方。

但是這個常數如果擺在下一篇要講的感知器（perceptron）當中的話，那就有不同的解釋了，這個留到下回再說。

那麼，基礎的部份都在前面的文章內容中講完了，剩下的要來說點什麼呢？

模型的統計面向

我們來講點這個模型的統計面向吧！

一般來說，我們在計算這個模型的時候，這個模型背後是有他的統計面向的假設的。

誤差

線性迴歸對誤差是有假設的，也就是假設誤差會呈現常態分佈（Gaussian distribution），這樣的假設與這個模型所使用的 mean square error 是有關係的，不過今天不會深入這些關係。

我們要進入這件事之前，我們先來看看常態分佈長什麼樣子。

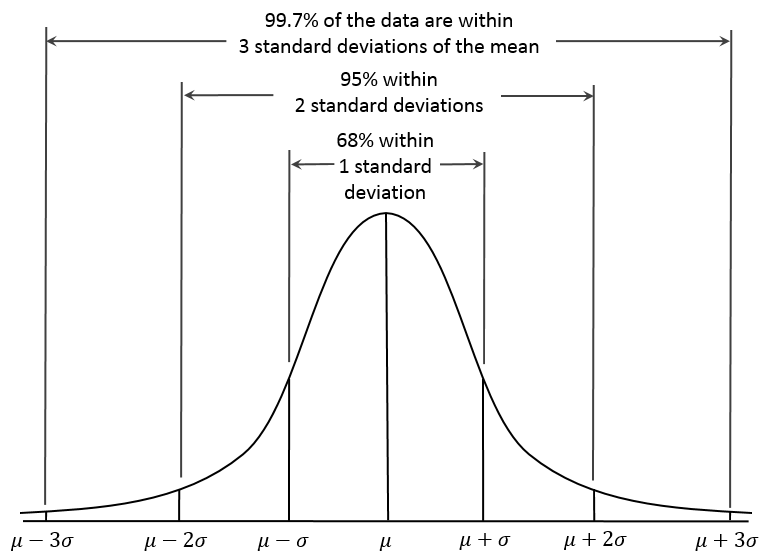
Wikipedia

我們借到了維基百科的圖，其中 X 軸是連續的數值，Y 軸是這些數值出現的機率或是頻率。你會看到他是以平均值 $\mu$ 為中心的一個分佈，整個分佈是單峰的。平均值的出現機率是最高的，機率開始往兩邊遞減。這說明了最常出現的數值會剛好在平均值上，其他離平均值很遠的數值也是有機率出現，但是機率很小。

整個分佈的寬度是由標準差 $\sigma$ 的大小決定的，如果標準差愈大，代表這個分佈是愈寬的，愈寬代表資料的離散程度是大的。

這其實來自於對於自然現象的觀察。高爾頓，達爾文的表弟，觀察了自然現象，發現眾多自然現象都有一種趨勢，像是人的身高跟體重都是連續的數值，而且都沒有上下界，為什麼他們不會平均分佈呢？他會向某一個值集中，那個值差不多是整個分佈的平均值，這樣的趨勢被他稱為「迴歸」。這也是迴歸這個詞的由來，但今日的迴歸的意義不相同。

題外話，高爾頓提出了不少對今日的科學有影響的主張，像是他主張人類的才能是可以透過遺傳延續的，並提倡了優生學。他發表了一些關於指紋的研究，被認為跟今日以指紋鑑定有相關。在統計學上，他也發表了相關係數的概念，並且沿用至今。

以下是常態分佈的公式：

$$
P(x; \mu, \sigma) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{- \frac{(x - \mu)^2}{2 \sigma^2}}
$$

整體看起來可能很醜很複雜，我們通常會把平均值歸零，並且讓標準差為 1，他看起來就會簡潔許多。

$$
P(x; 0, 1) = \frac{1}{\sqrt{2 \pi}} e^{- \frac{x^2}{2}}
$$

大家注意一下，在常態分佈的公式中他的主要組成為一個 e 的指數，並且在指數項上有 $x^2$ 項。這些我們以後會用到。

平均就是最有可能出現的

那回到線性迴歸，線性回歸是怎麼做出預測的呢？

當假設了誤差的分佈是常態分佈之後呢？那麼就可以拿最常出現的那個值作為整個分佈的代表，數學上證明那個值剛好是平均值。

可以參考上圖，資料在 X 軸上分佈，當我們切了某個點 $x_i$ 來看，那麼 Y 軸上就會有不同資料點的誤差存在。縱使真實資料是有誤差的，我們知道這些誤差會遵從常態分佈，所以這些誤差的平均就可以作為一種預測值。

從上面我們提到的迴歸效應，我們知道用這些誤差的平均值作為預測是相對合理的。

數學上是這樣運作的，當我們今天有新的資料點要預測，那麼我們代入 $y = \mathbf{w}^T\mathbf{x} + b$ 公式中，算出來的其實是 Y 軸的平均值 $\hat{y_i}$。

這就是線性迴歸的假設了。

誤差的"寬度"是一樣的

在線性迴歸的假設上還有另一點，就是我們在每個不同 x 的切面上，誤差的寬度（標準差）都是一樣的。

如圖所示，我不確定是為了讓模型簡單好計算還是什麼原因。

今天的介紹就到這邊啦！