Functions

Function 會是在數學上常常看到的概念，但他到底是什麼？Function 常常被視為兩個集合之間對映的規則。我們先來定義對映的規則（rule of assignment）：

Def.

$$
two \enspace sets \enspace C, D, r \subseteq C \times D, \forall c \in C , d \in D,
$$

$$
\exists \enspace at \enspace most \enspace one \enspace (c, d) \in r
$$

所以如果當兩個對映關係（如下）有相同的第一分量 $c$，那他們其實是同一個對映關係，並且第二分量也會相同。

$$
[ (c, d) \in r, (c, d’) \in r ] \rightarrow [ d = d’ ]
$$

給定一個對映規則 $r$，定義域（domain） 也就是 $C$ 的子集合，他包含了所有 $r$ 中的第一分量。

Def.

$$
domain \enspace r = \{c \mid \exists d \in D \enspace s.t. \enspace (c, d) \in r \}
$$

相對，**值域（image）**是 $D$ 的子集合，他包含了所有 $r$ 中的第二分量。

Def.

$$
image \enspace r = \{d \mid \exists c \in C \enspace s.t. \enspace (c, d) \in r \}
$$

現在我們把所有需要的東西都定義好了，那函數（function） 的定義就會是一個對映規則，以及一個 set $B$ 包含了 $image \enspace r$，稱為函數的 對應域（codomain） ，而函數的 domain $A$ 也就是 $domain \enspace r$，函數的值域就是 $image \enspace r$ ，我們會以下列表示法表示：

$$
f: A \rightarrow B
$$

這表示他是一個從 $A$ map 到 $B$ 的函數。有時候我們會想像成在空間上的轉換，將 $A$ 上的點對映到 $B$ 上的點。我們會以 $f(a)$ 來代表 $f$ 在 $a$ 點的值（value）。

我們可以在函數上定義限制（restriction）：

Def.

$$
A_0 \enspace is \enspace the \enspace restriction \enspace of \enspace f
$$

$$
f: A \rightarrow B, A_0 \subseteq A \enspace s.t. \enspace f = \{ (a, f(a)) \mid a \in A_0 \}
$$

我們可以藉由限制（restriction）來限制我們的函數形式。我們還有另外一個方法，合成函數（function composition）：

Def.

$$
g \circ f \enspace is \enspace the \enspace composite \enspace of \enspace function \enspace f \enspace and \enspace g
$$

$$
f: A \rightarrow B, g: B \rightarrow C, g \circ f: A \rightarrow C, (g \circ f)(a) = g(f(a))
$$

$$
g \circ f = \{(a, c) \mid b \in B, f(a) = b, g(b) = c \}
$$

from Wikipedia

接著我們來討論一些不同的函數。

如果一個函數 $f: A \rightarrow B$ 是單射的（injective），或是一對一（one-to-one），那也就是說在 $A$ 中，不同的點會對映到不同的 像（image） 的。

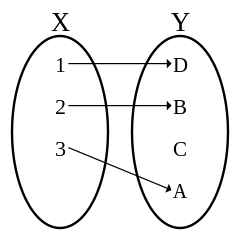
from Wikipedia

如果一個函數 $f: A \rightarrow B$ 是滿射的（surjective），或是映成（onto），那也就是說每個在 $B$ 中的元素都有被對映到。

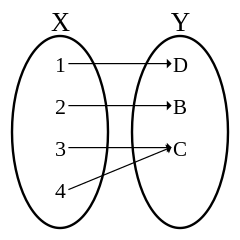
from Wikipedia

如果一個函數 $f: A \rightarrow B$ 是雙射的（bijective），那也就是說這個函數同時滿足 單射的（injective） 以及 滿射的（surjective）。

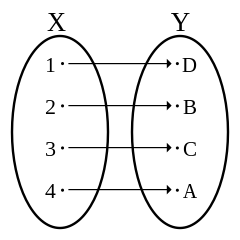
from Wikipedia

兩個 injective function 的 composite 是個 injective function。兩個 surjective function 的 composite 是個 surjective function。兩個 bijective function 的 composite 是個 bijective function。

那如果 function $f$ 是 bijective，那麼他的 反函數（inverse） 存在，也就是：
$$
f: A \rightarrow B, f \enspace is \enspace bijective, \exists
f^{-1}
$$

$$
s.t. \enspace f^{-1}(b) = a, a \in A, b \in B
$$

反函數有一個特性就是， $f$ 的反函數為 $f^{-1}$，而 $f^{-1}$ 本身也是雙射的，所以他的反函數也存在，他的反函數則是 $f$。

那如果要證明一個函數是 bijective 的話，那以下Lemma 會有幫助：

Lemma

$$
f: A \rightarrow B, \exists g: B \rightarrow A, \exists h: B \rightarrow A
$$

$$
s.t. \enspace \forall a \in A, g(f(a)) = a, \forall b \in B, f(h(b)) = b,
$$

$$
then \enspace g = h = f^{-1} \enspace is \enspace bijective.
$$

接下來，我們來討論一下 像（image）：

Def.

$$
f: A \rightarrow B, A_0 \subseteq A, the \enspace image \enspace of \enspace A_0 \enspace of \enspace f \enspace is
$$

$$
f(A_0) = \{ b \mid b = f(a) \enspace for \enspace at \enspace least \enspace one \enspace a \in A_0 \}
$$

另一方面，我們可以討論像的 原像（preimage）：

Def.

$$
f: A \rightarrow B, B_0 \subseteq B, f^{-1}(B_0) = \{ a \mid f(a) \in B_0\}
$$

$$
f^{-1}(B_0) \enspace is \enspace the \enspace preimage \enspace of \enspace B_0 \enspace under \enspace f.
$$

如果 $f: A \rightarrow B$ 是 bijective， $B_0 \subseteq B$，我們對 $f^{-1}(B_0)$ 有兩種解釋，他可以是 preimage of $B_0$ under $f$ ，或者是 image of $B_0$ under $f^{-1}: B \rightarrow A$。

在使用 $f$ 及 $f^{-1}$ 上需要小心。如果是 $f^{-1}$ 應用在 $B$ 的子集合上，他有很好的行為，他保留了包含、聯集、交集、差集的特性。我們應該要常用他。如果是 $f$ 應用在 $A$ 的子集合上，他只保留了包含及聯集的特性。

另一個需要小心的，以下兩個並不是總是為真：

$$
f^{-1}(f(A_0)) = A_0
$$

$$
f(f^{-1}(B_0)) = B_0
$$

結論是這樣的，如果 $f: A \rightarrow B, A_0 \subseteq A, B_0 \subseteq B$，則以下成立：

$$
A_0 \subseteq f^{-1}(f(A_0))
$$

$$
f(f^{-1}(B_0)) \subseteq B_0
$$

第一條式子的等號成立的條件為 $f$ 是 injective，第二條式子的等號成立的條件為 $f$ 是 surjective。